Испытание на разрыв и сжатие

Испытание на растяжение

При испытании на растяжение, определяют сопротивление металла малым пластическим деформациям, характеризующееся пределом пропорциональности σ_пц, пределам упругости σ_у и пределом текучести σ_т (или σ_0,2), а также сопротивление значительным пластическим деформациям, которое выражают временным сопротивлением σ_в.

При растяжении определяют и пластичность металла, то есть величину пластической деформации до разрушения, которая может быть оценена относительным удлинением образца δ и его относительным сужением ψ (после разрыва образца).

Для испытания на растяжение используют стандартные образцы (см. ниже). Машина для испытаний снабжена устройством, записывающим диаграмму растяжения.

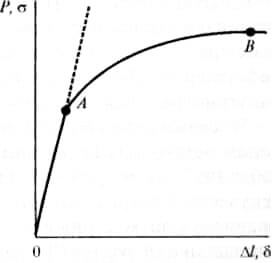
Диаграмма растяжения показывает зависимость между растягивающей нагрузкой, действующей на образец, и его деформацией. На диаграмме по оси ординат записывают нагрузку Р, а по оси абсцисс – абсолютное удлинение образца Δl (Δl = l_х — lо, где l_х и lо – текущая (в данный момент времени) и начальная длины образца) — рис. 1.

Схема диаграммы растяжения: изменение удлинения образца в зависимости от нагрузки

Кривая изменения абсолютного удлинения Δl в зависимости от прилагаемой нагрузки Р при растяжении состоит из прямолинейного  участка ОА и криволинейного АВ, отвечающего переходу в область пластических (остаточных) деформаций и характеризуемой постепенным уменьшением тангенса угла наклона кривой к оси абсцисс (см. рис. 1).

Пластической называют деформацию, остающуюся после снятия нагрузки (кроме того, наблюдается обратимая пластическая деформация, которая, как и упругая, исчезает после снятия нагрузки). Величина остаточной деформации в момент раз рушения (удлинение, сужение) служит мерой пластичности материала. Если величина пластической деформации до разрушении мала, то материал называют хрупким. Пластическая деформация предшествует любому виду разрушения (вязкому или квазихрупкому), но при квазихрупком разрушении она весьма мала, локализована в микро- и субмикрообъемах и не выявляется при обычных методах измерения микродеформации. В этом последнем случае необходимо изыскание такиx условий испытания (скорости нагружения,температуры испытании и т. п.), при которых можно было бы выявить пластичность материала.

Для возможности сравнения результатов испытаний различных но размерам образцов целесообразно установить связь между удельными и относительными величинами, т. е. между условным напряжением σ, равным P/F₀, где P -растягивающая нагрузка (сила), F₀ — площадь поперечного сечения образца до испытания, и относительным удлинением δ, равным Δl/I₀, где Δl — абсолютное уд- шпение образца; I₀ – длина образца до испытания. Так как значении Р и Δl делятся на постоянные для данных условий испытания величины, то вид диаграммы, приведенной на рис. 1, не меняется (отличается только масштабом) при переходе от координат P – Δl  к координатам σ — δ.

Напряжения ниже точки А практически не вызывают измеримой остаточной деформации и относительно этой точки могут быть установлены (с определенным допуском на точность измеряемых деформаций) предел упругости σ_у, а также предел пропорциональности σ_пц. Здесь и далее напряжения получаются делением соответствующей нагрузки на F₀ — площадь поперечного сечения образца до испытания.

Предел упругости σ_у — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σ_у.

Предел пропорциональности σ_пц — условное напряжение, соответствующее отклонениям от линейного хода кривой деформации (от закона Гука), задаваемым определенным допуском (например, увеличением тангенса угла наклона кривой деформации к оси напряжения на 25 или 50% при переходе от прямолинейного участка к криволинейному).

Следует отметить, что для реальных поликристаллических металлов определение σ_у и σ_пц представляет значительные методические трудности, так как предусматривает измерение очень малых деформаций. Поэтому на практике чаще обращаются к такой характеристике, как условный предел текучести.

Условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величина (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ_0,2). Величину σ_0,2 определяют, правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести.

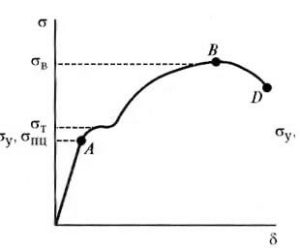
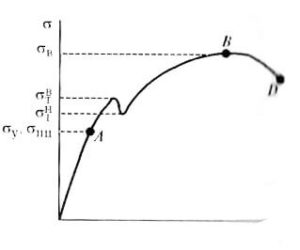
В тех случаях, когда диаграмма растяжения имеет площадку текучести (рис. 2а), измеряют физический предел текучести σ_т, условное напряжение, соответствующее наименьшей нагрузке площадки текучести, когда деформация образца происходит увеличения нагрузки. Иногда распространение деформации по длине образцов из пластичных материалов при напряжениях, отвечающих площадке текучести, носит волнообразный характер: вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс разшнми ся до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести (рис. 2б), вводят понятия о верхнем σ^в_т и нижнем σ^н_т пределах текучести.

Схемы диаграмм растяжения металлов, дающих площадку (а) зуб (б) текучести

Если при испытании образцов, например на растяжение, не возникает локализованной деформации (не образуется шейки – местное сужение поперечного сечения), то образец из хрупких металлов разрушается при какой-то максимальной нагрузке, отвечающей точке В на рис. 1. Деление этой нагрузки на площадь начального поперечного сечения дает разрушающее напряжение, называемое временным сопротивлением σ_b (это условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом). В тех случаях, когда окончание растяжения сопровождается местным утонением образца (образованием шейки), диаграмма растяжения имеет вид, изображенный на рис. 2, т. е. нагрузка в момент разрыва пластичного металла и напряжение, отнесенное к исходному сечению (в точке D), могут быть меньше, чем напряжение в какой-то предыдущий момент растяжения. Но и и этом случае временное сопротивление определяется применительно к точке В, т. е. относительно максимальной нагрузки, момент достижения которой практически совпадает с началом образования шейки в образце из пластичного материала. Появление шейки определяет переход от равномерной деформации всей  рабочей части образца к сосредоточенной деформации в определенном сечении.

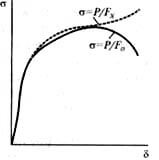
При переходе в область пластических деформаций (правее точки А на диаграмме рис. 1) изменения поперечного сечения образца становятся уже значительными и отнесение нагрузки к исходному (до деформации) сечению F₀ дает лишь условные напряжения. Если учитывать изменение сечения при деформации и относить нагрузку не к исходному сечению, а к сечению в каждый данный момент деформации F_x, то получают истинные напряжения. Эти последние, естественно, отличаются от условных напряжений и тем больше, чем пластичнее материал (чем сильнее изменяется сечение в ходе деформации относительно исходного). Соответственно изменяется вид диаграммы растяжения, которая схематично показана на рис. 3. В случае хрупких материалов (чугун, литые алюминиевые сплавы и др.) различие между истинными и условными напряжениями может быть небольшим.

По диаграмме растяжения, как было отмечено выше, можно судить и о пластичности металла, которая характеризуется относительным удлинением после разрыва δ и относительным сужением площади сечения у образца.

Под относительным удлинением δ понимают отношение абсолютного удлинения образца после разрыва Δl = l_к — lо (где l_к — конечная длина образца) к его начальной расчетной длине lо, выри женное в процентах, т. е.

δ =  (l_к – lо)*100%/lо

В случае испытания «коротких» (пятикратных) образцов (см. ниже) относительное удлинение обозначают δ₅, в случае «длинных» (десятикратных) – δ₁₀.

Относительное сужение после разрыва ψ представляет собой отношение уменьшения площади поперечного сечения разорванного образца ΔF= F₀ — F_K (где F_K – минимальная площадь поперечного сечения образца после его разрыва) к первоначальной площади поперечного сечения Fo, выраженное в процентах, т. е.

Ψ = (F₀ — F_K)*100%/ F₀

 При расчете режимов обжатий в процессах обработки меча им» давлением чаще всего используют показатель δ.

Тангенс угла наклона прямой ОА к оси абсцисс (см. рис. 1) характеризует модуль упругости материала Е = σ/δ (где δ – относительная деформация, равная Δl/l₀). Модуль упругости E определяет жесткость материала: интенсивность увеличения напряжения по мере увеличении упругой деформации. Физический смысл Е сводится к тому, что он характеризует сопротивляемость металла упругой деформации. Модуль упругости практически не зависит от структуры металла и определяется силами межатомной связи. Все другие механические свойства являются структурно чувствительными и изменяются в зависимости от структуры в широких пределах.

Условное изображение диаграммы растяжения (сплошная линия) и диаграммы истинных напряжений (штриховая линия)

Следует отметить, что закон пропорциональности между напряжением и деформацией является справедливым лишь в первом приближении. При точных измерениях даже при небольших напряжениях в упругой области наблюдаются отклонения от закона пропорциональности. Это явление называют неупругостью. Оно проявляется в том, что деформация, оставаясь обратимой, отстает по фазе от действующего напряжения. В связи с этим при нагрузке-разгрузке на диаграмме растяжения вместо прямой линии получается петля гистерезиса, так как линии нагрузки и разгрузки не совпадают между собой.

Механические свойства металлов в испытаниях на растяжение определяют, используя стандартные образцы, общий вид которых показан на рис. 4.

Необходимо строго соблюдать определенные соотношения между начальной расчетной длиной образца l₀ и начальной площадью поперечного сечения в рабочей части образца F₀. Используют образцы двух видов: цилиндрические и плоские. Оба вида образном для испытания на растяжение применяют с начальной расчетной длиной lо = 5,65√F₀ или lо = 11,3√F₀ диаметром do = 3…25 мм или толщиной а_о = 0,5. ..25 мм и шириной b₀ = 20…30 мм. При ном образцы с расчетной длиной lо = 5, √F₀ именуются «короткими», а образцы с lо = 11,3 √F₀ – «длинными», причем применение первых предпочтительнее. Литые образцы и образцы из хрупких металлов допускается изготавливать с начальной расчетной длиной lо = 2,82√F₀.

В случае цилиндрических образцов в качестве основных применяют образцы с диаметром do = 10 мм и начальной расчетной длиной l₀ = 5do (короткие) и lо = 10d₀ (длинные); в первом случае поручаемое значение относительного удлинения после разрыва обозначают δ₅, во втором – δ₁₀.

Общий вид стандартных образцов для испытания на растяжение: а -цилиндрический образец; б — плоский

Испытание на сжатие

Испытание на сжатие обычно применяют для определения механических свойств хрупких материалов. Цилиндрические образцы диаметром 10…25 мм и высотой, равной диаметру, подвергают сжатию, фиксируя при этом упругие и остаточные деформации Торцовые поверхности образцов должны быть отшлифованы, плоскопараллельными и перпендикулярными к оси образца. Большое влияние на результаты испытания оказывает трение на торцах об разцов. Для уменьшения трения применяют специальные прокладки (свинцовые) или смазку торцов.

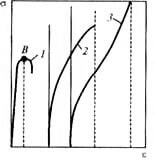
Испытание на сжатие производят на тех же машинах, что и испытание на растяжение, с использованием приспособлений (реверсов) для превращения растягивающей нагрузки в сжимающую. При испытании на сжатие получают диаграмму сжатия (рис. 5), по которой определяют основные механические характеристики испытуемого материала. В процессе сжатия образца из пластичного металла при напряжении ниже предела текучести металл ведет так же, как и при растяжении. После достижения предела текучести образец пластически деформируется, принимая бочкообразную форму. При смазке торцов или наличии мягких прокладок на торцах деформация образца по высоте получается более равномерной.

При испытании на сжатие пластичных металлов (см. рис. 5 кривые 2 и 3) обычно определяют пределы пропорциональности и текучести как при испытании на растяжений, а степень осадки (относительную деформацию) находят из соотношения:

ε = (h₀-h₁)*100%/h₀

 где hо и h1 — высоты образца до и после осадки.

Сравнительные схемы диаграмм сжатия различных металлов: 1 – чугун; 2 – медь; 3 – сталь

В случае испытания на сжатие хрупких металлов (см., например, рис. 5, кривая 1) достижение в точке В напряжения σ_в сопровождается разрушением образца. Разрушение образца обычно происходит под углом 45° к линии действия сжимающей силы.